T test và anova có cùng mục đích là kiểm định sự khác biệt về giá trị trung bình giữa các nhóm được test. Cụ thể ở đây là Independent sample t test và Oneway anova.
Ví dụ cần sử dụng t test và anova để kiểm định
Ví dụ 1 : Cần kiểm định về sự Hài Lòng trong công việc giữa hai nhóm giới tính Nam/Nữ. Mục đích là xem nhóm giới tính nào hài lòng trong công việc hơn, nghĩa là nhóm đó có điểm trung bình về Hài Lòng cao hơn nhóm còn lại
Ví dụ 2 : Hoặc kiểm định về sự Hài Lòng trong công việc giữa giữa 3 nhóm tuổi: <30 tuổi, từ 30-40 tuổi, trên 40 tuổi. Mục đích là xem nhóm tuổi nào hài lòng trong công việc hơn, nghĩa là nhóm đó có điểm trung bình về Hài Lòng cao hơn các nhóm còn lại.
Sự khác nhau giữa t test và anova:
T test chỉ kiểm định được cho biến có hai nhóm quan sát, còn anova kiểm định được cho biến có từ 2 biến quan sát trở lên, ví dụ 2 3 4 5 nhóm…
Sự giống nhau giữa t test và anova:
Cả hai loại thống kê này đều dùng để kiểm định giá trị trung bình. Nếu biến cần kiểm định chỉ có hai nhóm quan sát thì có thể áp dụng t test hoặc anova để kiểm định, giá trị kết quả hiển thị sẽ giống y hệt nhau.
Independent Samples T-Test dùng tương tự như phân tích ANOVA, tuy nhiên hạn chế là chỉ so sánh được 2 nhóm với nhau. Ví dụ dùng so sánh có sự khác biệt giữa các nhóm giới tính( nam, nữ) với sự hài lòng(thang đo likert 5 điểm) hay không. Nhóm MBA hotrospss@gmail.com giới thiệu cách thức làm bằng thao tác hình ảnh minh họa, và bằng video.
CÁCH THỨC TIẾN HÀNH KIỂM ĐỊNH GIẢ THUYẾT VỀ TRỊ TRUNG BÌNH CỦA 2 TỔNG THỂ ĐỘC LẬP (Independent Samples T-test)
Ví dụ này so sánh có sự khác biệt về sự Hài Lòng giữa hai nhóm Tuổi ( <30 , >30) hay không. Ta có hai biến là biến HAILONG và biến DOTUOI
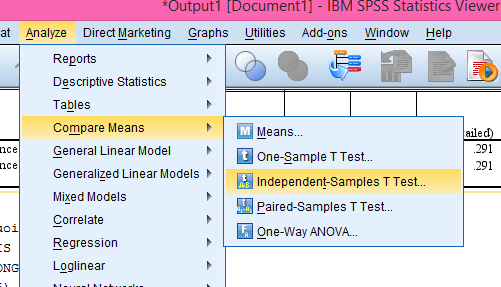
Vào menu Analyze -> Compare Means -> Independent-samples T-test
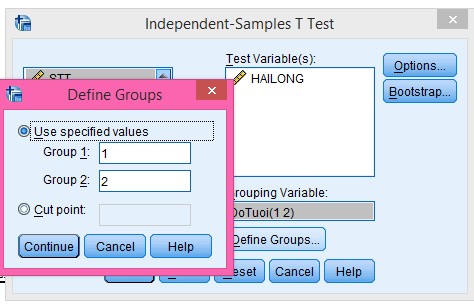
Chọn biến định lượng cần kiểm định trị trung bình đưa vào khung Test Variable(s).
Chọn biến định tính chia số quan sát thành 2 nhóm mẫu để so sánh giữa 2 nhóm này với nhau đưa vào khung Grouping Variable.
Chọn Define Groups… để nhập mã số của 2 nhóm. Click Continue để trở lại hộp thoại chính -> Click Ok để thực hiện lệnh.
Trong kiểm định Independent-samples T-test, ta cần dựa vào kết quả kiểm định sự bằng nhau của 2 phương sai tổng thể (kiểm định Levene). Phương sai diễn tả mức độ đồng đều hoặc không đồng đều (độ phân tán) của dữ liệu quan sát.
Nếu giá trị Sig. trong kiểm định Levene (kiểm định F) < 0.05 thì phương sai của 2 tổng thể khác nhau, ta sử dụng kết quả kiểm định t ở dòng Equal variances not assumed.
Nếu Sig. ≥ 0.05 thì phương sai của 2 tổng thể không khác nhau, ta sử dụng kết quả kiểm định t ở dòng Equal variances assumed.
Trong ví dụ trên Sig. của kiểm định F = 0.494 > 0.05 -> chấp nhận giả thuyết H0: không có sự khác nhau về phương sai của 2 tổng thể -> sử dụng kết quả ở dòng Equal variances assumed.
Nếu Sig. của kiểm định t ≤ α (mức ý nghĩa) -> có sự khác biệt có ý nghĩa về trung bình của 2 tổng thể.
Nếu Sig. > α (mức ý nghĩa) -> không có sự khác biệt có ý nghĩa về trung bình của 2 tổng thể.
Trong ví dụ trên sig. = 0.291 > 0.05 -> không có sự khác biệt có ý nghĩa về trung bình của 2
tổng thể.
Video hướng dẫn thao tác:
https://youtu.be/mEtQnWiyuIA
One way anova là gì?
Phân tích phương sai một yếu tố ( còn gọi là oneway anova) dùng để kiểm định giả thuyết trung bình bằng nhau của các nhóm mẫu với khả năng phạm sai lầm chỉ là 5%.
Ví dụ: Phân tích sự khác biệt giữa các thuộc tính khách hàng (giới tính, tuổi, nghề nghiệp, thu nhập…) đối với 1 vấn đề nào đó (thường chọn là nhân tố phụ thuộc, vd: sự hài lòng).
Bài này sẽ đề cập về lý thuyết, thực hành từng bước phân tích phương sai một yếu tố anova, cách diễn giải kết quả, ý nghĩa các chỉ số trong anova.
Một số giả định khi phân tích ANOVA:
– Các nhóm so sánh phải độc lập và được chọn một cách ngẫu nhiên.
– Các nhóm so sánh phải có phân phối chuẩn or cỡ mẫu phải đủ lớn để được xem như tiệm cận phân phối chuẩn.
– Phương sai của các nhóm so sánh phải đồng nhất.
Lưu ý: nếu giả định tổng thể có phân phối chuẩn với phương sai bằng nhau không đáp ứng được thì bạn có thể dùng kiểm định phi tham số Kruskal-Wallis sẽ để thay thế cho ANOVA.
Lý thuyết
Kết quả kiểm định gồm hai phần:
Phần 1:
Levene test: dùng kiểm định phương sai bằng nhau hay không giữa các nhóm
Ho: “Phương sai bằng nhau”
Sig <= 0.05: bác bỏ Ho
Sig >0.05: chấp nhận Ho -> đủ điều kiện để phân tích tiếp anova
Phần 2:
ANOVA test: Kiểm định anova
Ho: “Trung bình bằng nhau”
Sig <=0.05: bác bỏ Ho -> đủ điều kiện để khẳng định có sự khác biệt giữa các nhóm đối với biến phụ thuộc
Sig >0.05: chấp nhận Ho -> chưa đủ điều kiện để khẳng định có sự khác biệt giữa các nhóm đối với biến phụ thuộc
Khi có sự khác biệt thì có thể phân tích sâu hơn để tìm ra sự khác biệt như thế nào giữa các nhóm quan sát bằng các kiểm định Tukey, LSD, Bonferroni, Duncan như hình dưới. Kiểm định sâu anova gọi là kiểm định Post-Hoc
Cách thực hiện
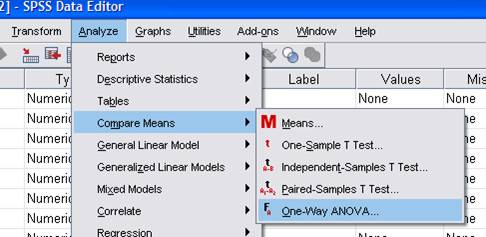
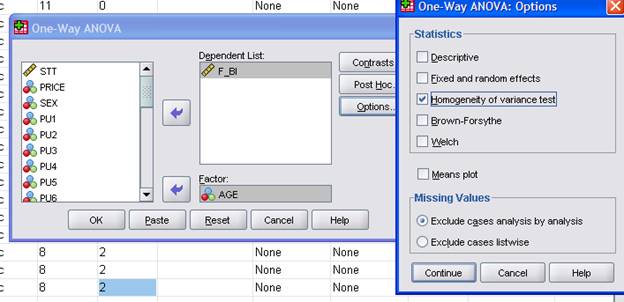
Phân tích anova : vào menu Analyze -> Compare Means -> One-Way ANOVA
Bấm vào option chọn Homegenety of variance test để kiểm định phương sai đồng nhất.
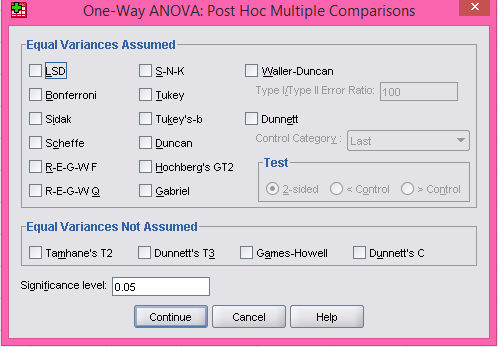
Nếu muốn kiểm định Post hoc thì ấn vào nút Post hoc để kiểm định sâu sau anova, bảng sau xuất hiện và chọn một trong những kiểm định posthoc:Tukey, LSD, Bonferroni, Duncan
Kết quả ANOVA ra như sau
Cách phân tích kết quả anova
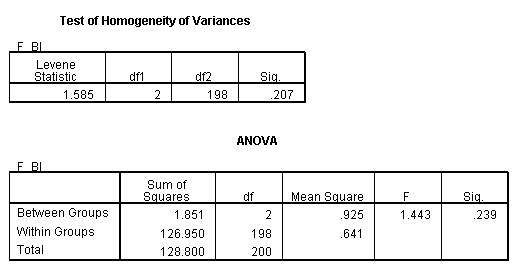
Viết tắt: F_BI Buying Intention: dự định mua hàng, Age: nhóm tuổi.
Kết quả này cho biết phương sai của dự định mua hàng có sự khác biệt giữa cácnhóm tuổi hay không. Nghĩa là phương sai của dự định mua hàng của nhóm tuổi này có khác phương sai của dự định mua hàng của nhóm tuổi kia hay không?
Sig của thống kê Levene = 0.207 (>0.05) nên ở độ tin cậy 95% giả thuyết H0: “Phương sai bằng nhau” được chấp nhận, và bác bỏ giả thuyết H1: “Phương sai khác nhau”. Và do đó kết quả phân tích ANOVA có thể sử dụng.
Kết quả phân tích ANOVA với mức ý nghĩa 0.239> 0.05, như vậy với dữ liệu quan sát chưa đủ điều kiện để khẳng định có sự khác biệt về dự định mua hàng giữa các nhóm tuổi.